LeetCode►算法

最大子数组和

最大子数组和

就快要秋招了，又该准备刷题了。其实一直都很反感刷题这件事，大一的时候就刷OJ，找实习的时候刷LeetCode，找工作的时候也刷，考研的时候又刷一回，现在又得再刷一回。刷题这事吧，挺花时间，但是收益并不高，这几天刷题，过几天去忙点其他事，基本就忘得差不多了。很无奈，你不刷，企业就觉得你基础不行，coding不行。想想后面还得再回去看八股文，头都大了，计算机专业课，可以说也是反反复复学了好多遍吧，也是学了忘，忘了学，但是实际用上的知识，不多。

这是上个月的事情了。信软的妹妹给我发来一道题，LeetCode的第53题，最大子数组和。这个题目要求在一个给定的整数数组中，找到一个连续子区间，使得子区间中元素的和最大。

既然是妹妹发的，那肯定不能做不出来，一时间胜负欲拉满。我当时看完题目的时候，坚信用双指针能解出来。理由是，要寻找的子区间是一个连续的区间，两个指针之间也是连续的子区间，如果能够通过移动两个指针，使它们逐步向目标子数组靠近，不就可以解决了吗？

一开始是想着能不能只经过一次遍历，就能找到最大子数组和呢？先初始化左右指针，初始时刻都指向数组首元素，结合滑动窗口的思想，右指针不断右移，扩大窗口的大小，左指针也向右移动，但是不超过右指针，维护一个求和的变量，右指针每移动一次，就把指向的元素加进来，左指针每移动一次，就把指向的元素减去，这样，求和变量就能记录窗口中元素的和，只需要找到目标窗口就可以了，也就是什么时候右指针该移动，什么时候左指针该移动的事了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int size = nums.size();
        int max = nums[0];
        int cur = nums[0];

        int i = 0, j = 0;
        for (int k = 1; k < size; k++)
        {
            cur = cur + nums[k];
            if (cur > max)
            {
                max = cur;
                j = k;
            }
        }

        cur = max;
        for (int k = 0; k < j; k++)
        {
            cur = cur - nums[k];

            if (cur > max)
            {
                max = cur;
                i = k;
            }
        }

        return max;
    }
};

这是一开始的想法，右指针一路狂奔，在狂奔的过程中记录最大和，然后左指针再追赶右指针，进一步缩小子区间的长度。这个思路看起来好像没啥问题，提交的时候信心满满，结果也就A了一部分的测试样例而已。

问题在于max被初始化为nums[0]了，题目中给定的整数数组是允许出现负数的，但当数组元素全是负数且按照递增顺序排列时，如[-2, -1]，上面的代码就不work了，因为往右走元素和会越来越小，max一直是nums[0]的值。

接下来就开始走歪路了，想着把数组元素全是负数（或者0）且按照递增顺序排列的这种情况做特殊处理：

1
2
3
4
5
6
7
8
9
10
11
12
13
int k = 1;
for (; k < size; k++)
{
    int a = nums[k];
    int b = nums[k - 1];
    if (a <= 0 && b <= 0 && a >= b)
        continue;
    else
        break;
}

if (k >= size)
    return nums[size - 1];

再一提交，很好，现在数组元素全是负数（或者0）且按照递增顺序排列的这种情况解决了，但是，如果数组不是有序的，比如，[-2, -3, -1]就不在上述代码的处理范围之内了，前面的[-2, -3]仍然阻碍了max变量的更新。那这样的话，直接不管顺序了，如果数组全是负数，找最大值就行了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int max = nums[0];
int k = 1;
for (; k < size; k++)
{
    int temp = nums[k];
    if (temp <= 0)
    {
        if (temp > max)
            max = temp;
    }
    else
        break;
}

if (k >= size)
    return max;

处理完数组元素全是负数的情况，又出现了左侧负数和太大导致max依旧不能正常更新的情况，如数组[0, -3, 1, 1]，最大和子数组是[1, 1]，但是右指针根本就没有移动过。处理这种情况的思路简单又粗暴，把数组逆向再处理一遍就好了，然后再取两个方向找到的子数组和的最大值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int size = nums.size();

        int max = nums[0];
        int k = 1;
        for (; k < size; k++)
        {
            int temp = nums[k];
            if (temp <= 0)
            {
                if (temp > max)
                    max = temp;
            }
            else
                break;
        }

        if (k >= size)
            return max;

        int max1 = nums[0];
        int cur = nums[0];

        int i = 0, j = 0;
        for (int k = 1; k < size; k++)
        {
            cur = cur + nums[k];
            if (cur >= max1)
            {
                max1 = cur;
                j = k;
            }
        }

        cur = max1;
        for (int k = 0; k < j; k++)
        {
            cur = cur - nums[k];

            if (cur > max1)
            {
                max1 = cur;
                i = k;
            }
        }



        int max2 = nums[size-1];
        cur = nums[size-1];

        i = size-1;
        j = size-1;
        for (int k = size-2; k >= 0; k--)
        {
            cur = cur + nums[k];
            if (cur >= max2)
            {
                max2 = cur;
                j = k;
            }
        }

        cur = max2;
        for (int k = size-1; k > j; k--)
        {
            cur = cur - nums[k];

            if (cur > max2)
            {
                max2 = cur;
                i = k;
            }
        }

        return max1 > max2 ? max1 : max2;
    }
};

做到这里，我已经不管一次遍历就能解决的事情了，只想赶紧A完给妹妹看。这一次最大元素和的子数组不在最左边，也不在最右边了，是夹在数组中间了，比如数组[0,-3,-2,-3,-2,2,-3,0,1,-1]，其最大和子数组是[2]，双向处理的方式也失效了。

这下想不出其他方法了，做到这里花了快一个小时了，只能先吃个饭，顺便想想有没有其他控制指针移动的条件。后来实在是想不出来了，去看了一下评论区，发现有一个很优雅的答案，很符合我对一次遍历数组就能解决问题的完美期待。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int res = nums[0];
        int sum = 0;
        for (auto x : nums)
        {
            sum += x;
            res = max(res, sum);
            if (sum <= 0)
                sum = 0;
        }
        return res;
    }
};

但是这段代码读起来晦涩难懂，取最大值可以理解，但是为什么sum <= 0的时候要重新置零呢？这跟找最大子数组和有什么关系呢？

这段代码中，其实是维护了一个滑动窗口，并不断更新窗口中元素的最大和。当窗口内的元素和小于或者等于零时，丢弃该窗口。显然，该窗口中的元素是原数组的一个连续子区间，sum变量记录了窗口起始元素到窗口结束元素之间所有元素的累计和，res变量则记录了从窗口起始元素开始，到窗口结束元素之间所有元素的最大累计和。注意到，sum的值是可能小于res的，比如，在求累积和的过程中又加入了一个负数。

这个算法可以处理上面提到的数组元素全是负数的情况吗？答案是肯定的，证明如下：

证：给定一个序列，，此时最长子数组的长度为1，对应元素为数组中的最大值。在上述算法中，sum的值总是小于或等于零，该算法退化为找最大值的算法，证毕！

max的值记录的是从窗口起始元素开始，到窗口结束元素之间所有元素的最大累计和，当sum <= 0时，算法很自信地把窗口给丢弃了，我的疑问是，有没有可能窗口中存在一个连续的子区间，其元素和比res还要大？答案是不可能，证明如下：

证：给一个序列，，且存在，当时，有。此时对于子序列，算法逻辑为上述已证明的找最大值算法。对于窗口大小大于或者等于2的窗口，其首元素不可能是负数或者0。因此，只需考虑窗口的首元素为正数的情况。作序列的累计和曲线，由图可知序列中不存在比res更大的连续子数组和。

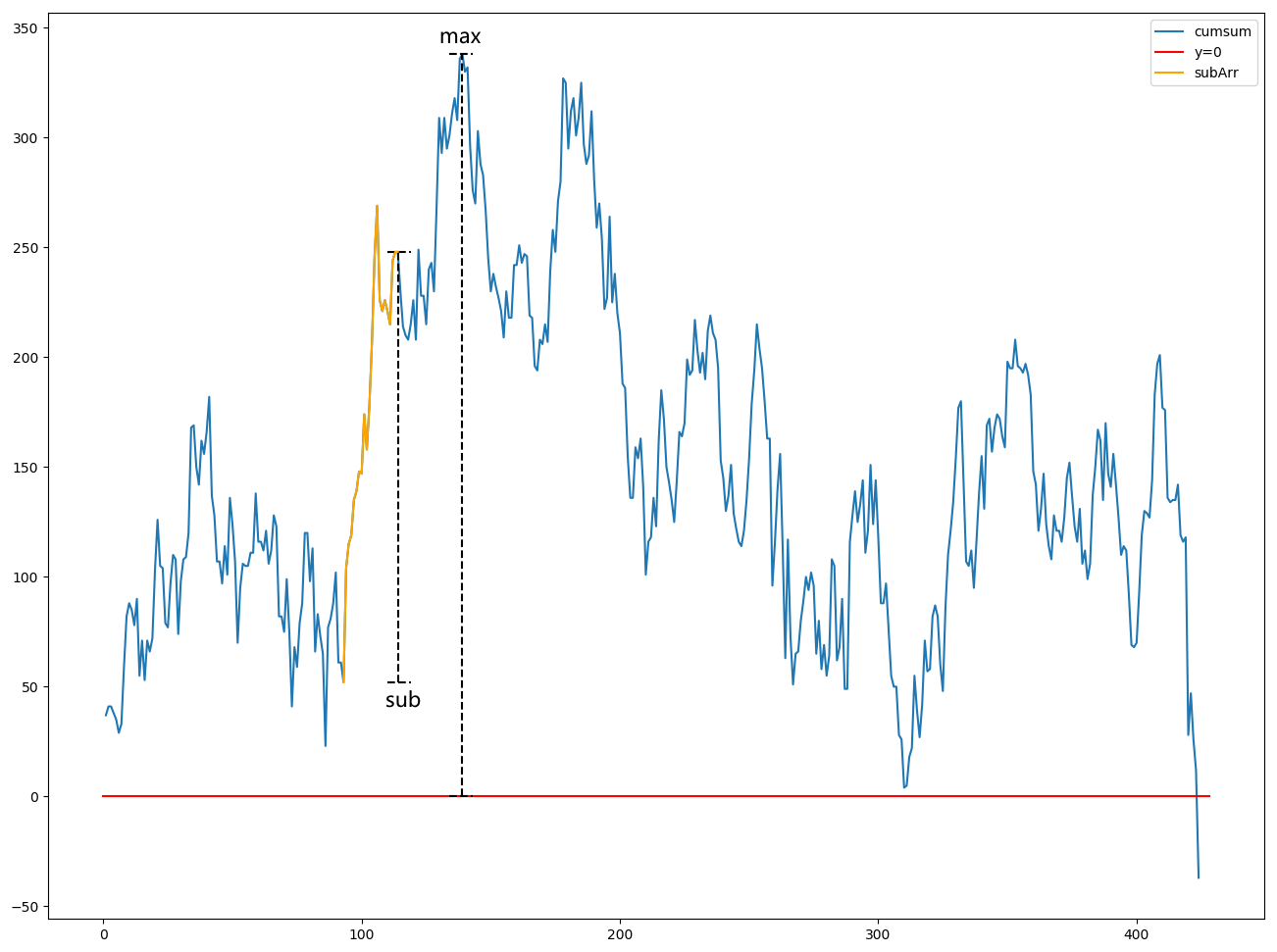
另外的一个问题是，窗口中的后半段的连续元素与数组后续的元素组成的连续子数组，其元素和有没有可能比res还要大？只要存在这样的连续子数组，那么当前窗口就不能随意丢弃。答案是可能存在，但当前窗口仍然可以丢弃。证明如下：

证：窗口中任取一元素，可知，不妨记从开始到窗口结束元素的累积和为，的值一定小于或者等于sum的值。由于sum的值最后小于或等于零，则数组后续的元素至少需要提供与res相等的连续子数组和，才有可能对res进行更新，此时，将窗口内的元素丢弃，留下数组后续的元素组成的连续子数组，其元素和将不少于res，因此，当前窗口可以直接丢弃。

这道题整整折腾了好几个小时才想明白，一共提交了N才成功A过去：

虽然代码不是自己想的，但也是自己想办法证明的，觉得还是挺值得记录下来的，也证明我是真的有在刷题的，虽然秋招笔试面试的时候可能一道题也做不出来。